链表
Jiacheng / 2018-03-15
链表
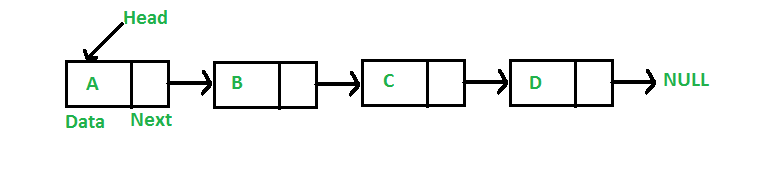
与数组一样,链表也是一种线性数据结构。 与数组不同,链表元素的存储空间是不连续的;元素之间使用指针链接,即前一个元素使用指针(后继指针 next)保存下一个元素的地址。链表元素与指针共同成为链表的节点(Node)
为什么要用链表?
数组可以用来存储类似类型的线性数据,但是数组有以下局限:
- 数组的大小是固定的:所以必须先确定元素数量的上限。 而且,通常情况下,无论需要使用的空间是多大,数组分配的内存大小都等于元素数量上限,而与使用情况无关。
- 在一个数组中插入一个新元素开销很大,因为需要为新元素创建空间,新元素后面的所有已存在的元素必须进行移位。
例如,在一个系统中, id [] 中保存一个已排序的 ID 数组:
id[] = [1000, 1010, 1050, 2000, 2040]
如果我们想插入一个新的 ID 1005,同时保持数组已排序,我们必须移动1000之后的所有元素(不包括1000)。 在不使用某些特殊技术得情况下,删除元素的开销也很大。 例如,要删除 id []中的1010,1010之后的所有内容都必须移动。
数组和链表的主要区别
- 数组是包含相似类型数据元素集合的数据结构,而链表则被视为非基本的数据结构,包含称为节点的无序元素集合。
- 在数组中,使用索引访问元素,即,如果要进入第四个元素,则必须在方括号内写入变量名称及其索引或位置。
- 但是,在一个链表中,你必须从头开始,一个节点一个节点地往后查找,直到访问到第四个元素。
- 访问数组中的元素很快,而访问链表重的元素需要\(O(n)\)(linear time)的时间复杂度,因此速度要慢一些。
- 在数组中,插入和删除元素的操作需要耗费不少的时间,但是在链表中这两个操作就很快。
- 数组的大小是固定的,而链表是动态、可扩展的,可以扩展或缩小大小。
- 对于数组,其内存是在编译期间分配,而链表,内存在执行或运行时分配。
- 数组中元素是连续存储的,而在链表中是随机存储的。
- 由于实际数据存储在数组中的索引中,因此消耗的内存较少。 相反,链表中节点存储了额外的下一个和前一个节点的引用(双向链表),因此链表需要的内存比数组要多。
- 此外,数组中内存利用效率比较低。 相反,链表中内存利用率更高。
链表的优点
- 动态大小
- 易于插入 / 删除
链表的缺点
链表的表示形式
链表由指向链表第一个节点的指针表示。 第一个节点称为链表的头。 如果链表为空,那么 head 的值为 NULL。 列表中的每个节点至少由两部分组成:
- 数据
- 指向下一个节点的指针(或引用)
在 c 中,可以使用结构体表示一个节点。 下面是一个带有整数数据的链表节点的示例。 在 Java 或 Python 中,LinkedList 可以表示为一个类,而 Node 可以表示为一个单独的类。 LinkedList 类包含一个 Node 类型的引用。
Python 代码示例:
class Node:
def __init__(self, data):
self.data = data
self.next = None
class LinkedList:
def __init__(self):
self.head = None使用以上两个类创建一个有三个元素的链表:
def main():
linked_list = LinkedList()
linked_list.head = Node(1)
second_node = Node(2)
third_node = Node(3)
linked_list.head.next = second_node
second_node.next = third_node链表的遍历
遍历上面已创建的 linked_list
def print_list(linked_list):
temp = linked_list.head
while temp:
print(temp.data)
temp = temp.next插入节点
本章节代码准备参考上一章节
向链表中插入一个节点有三种方式:
- 在链表的最前面插入节点
- 在给定的节点之后插入节点
- 在链表的末尾插入节点
在链表的最前面插入节点
这种情况下,新节点总是插入在给定链表的 head 之前, 并且新添加的节点将成为链表的新的 head。 例如,如果给定的链表是 10->15->20->25,在最前面插入一个节点 5,那么链表就变成 5->10->15->20->25。
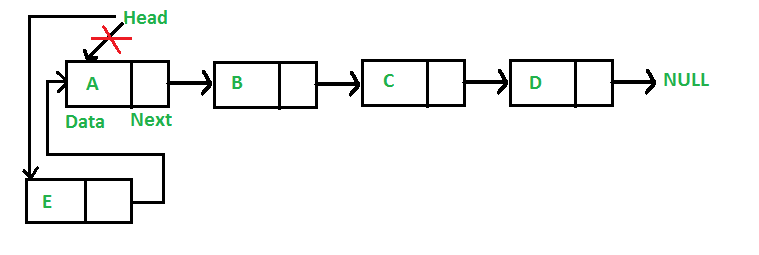
在上节定义 的 LinkedList 类里面定义 push() 方法,需要注意的是该方法需要接收指向链表原head 的指针,因为需要将 指向原 head 指针更改为指向新节点:
def push(self, new_data):
new_node = Node(new_data)
new_node.next = self.head
self.head = new_node 显然,push() 方法的时间复杂度为\(O(1)\)。
在给定节点的后面插入节点
给定一个节点,把新的节点插入在给定节点的后面
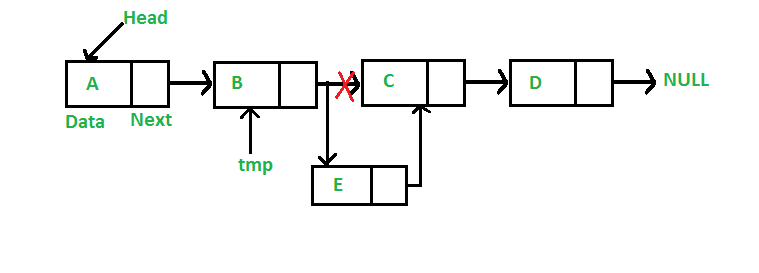
同样的,在 LinkedList 类里定义 insertAfter() 方法:
def insertAfter(self, prev_node, new_data):
if prev_node is None:
print "The given previous node must inLinkedList."
return
new_node = Node(new_data)
new_node.next = prev_node.next
prev_node.next = new_node 显然,insertafter()的时间复杂度也为\(O(1)\)。
在结尾添加一个节点
新节点总是添加在给定的链表的最后一个节点之后。 例如,如果给定的链表是 5->10->15->20->25,我们在末尾加上一个项目30,那么链表就变成 5->10->15->20->25->30。 由于链表通常由其 head 表示,因此我们必须遍历链表直到末尾,然后将最后一个节点的 next 指向为新节点。
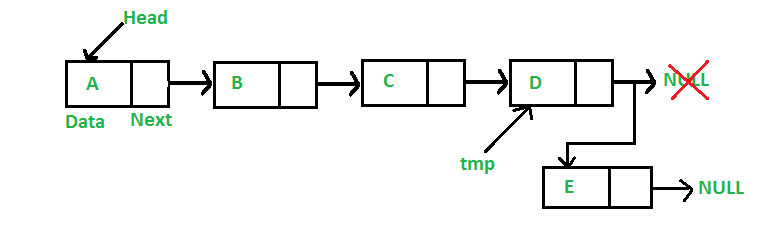
同样的,在 LinkedList 类里定义 append() 方法:
def append(self, new_data):
new_node = Node(new_data)
if self.head is None:
self.head = new_node
return
last = self.head
while (last.next):
last = last.next
last.next = new_node Time complexity of append is O(n) where n is the number of nodes in linked list. Since there is a loop from head to end, the function does O(n) work.
append()方法的时间复杂度为\(O(n)\),其中 n 是链表中的节点数。因为函数完成了对链表的一次遍历。
如果链表保留一个指向链表尾部的额外指针, append()方法的时间复杂度可以优化为\(O(1)\).
完整实现
下面是一个由 Node 类和 LinkedList 类组成的一个完整的链表实现 。
# Node class
class Node:
def __init__(self, data):
self.data = data # Assign data
self.next = None # Initialize next as null
# Linked List
class LinkedList:
def __init__(self):
self.head = None
def push(self, new_data):
new_node = Node(new_data)
new_node.next = self.head
self.head = new_node
def insertAfter(self, prev_node, new_data):
if prev_node is None:
print "The given previous node must inLinkedList."
return
new_node = Node(new_data)
new_node.next = prev_node.next
prev_node.next = new_node
def append(self, new_data):
new_node = Node(new_data)
if self.head is None:
self.head = new_node
return
last = self.head
while (last.next):
last = last.next
last.next = new_node
def printList(self):
temp = self.head
while (temp):
print temp.data,
temp = temp.next
局部性原理 Locality of Reference:处理器访问存储器时,无论是读取指令还是存取数据,所访问的存储单元在一段时间内都趋向于一个较小的连续区域中。空间局部(Spatial locality):紧邻被访问单元的地方也将被访问。 时间局部(Temporal locality):刚被访问的单元很快将再次被访问。↩
